Floating Ponint
aka.부동소수점
부동소수점(浮動小數點, floating point) 또는 떠돌이 소수점 방식은 실수를 컴퓨터상에서 근사하여 표현할 때 소수점의 위치를 고정하지 않고 그 위치를 나타내는 수를 따로 적는 것으로, 유효숫자를 나타내는 가수와 소수점의 위치를 풀이하는 지수로 나누어 표현한다.
Floating point in javascript
javascript에선 부동소수점(double-precision 64-bit binary format IEEE 754)으로 처리를 한다.
64-bit 방식을 ‘배정도’ 방식, 32-bit 방식을 ‘단정도’ 방식이라고 한다.
Floating point Pros/Cons
고정 소수점 방식과 비교!
Pros
- 고정 소수점 방식보다 넓은 범위의 수를 나타낼 수 있다.
Cons
-
근사값 표현이기 때문에 훨씬 부정확함
-
속도가 느림
0.1 + 0.2 !== 0.3 why?
오차가 생기는 이유는 간단히 말해
부동소수점 연산시 반올림으로 인해 오차가 발생하기 때문이다.
참고로 0.1 + 0.7 !== 0.8 이다
(0.7999999999999999가 답으로 나온다! 이 또한 부동 소수점 방식으로 인한 오차)
(모든 실수 계산은 조금식 오차가 있지만 무시할 수 있을 만큼의 적은 오차인 경우엔 결과로 생각되는 10진수로 처리된다고 한다.)
binary format
컴퓨터는 0, 1 밖에 이해하고 저장하지 못한다. (2진법)
비트(bit)란? - 컴퓨터에서 사용하는 가장 작은 데이터 단위, 하나의 비트는 2진수 1 또는 0으로 표현되어 데이터를 처리, 저장, 전송 할 때 사용된다.
예를 들어! 양의 정수를 2진수로 저장할땐, 아래와 같은 과정을 거친다.
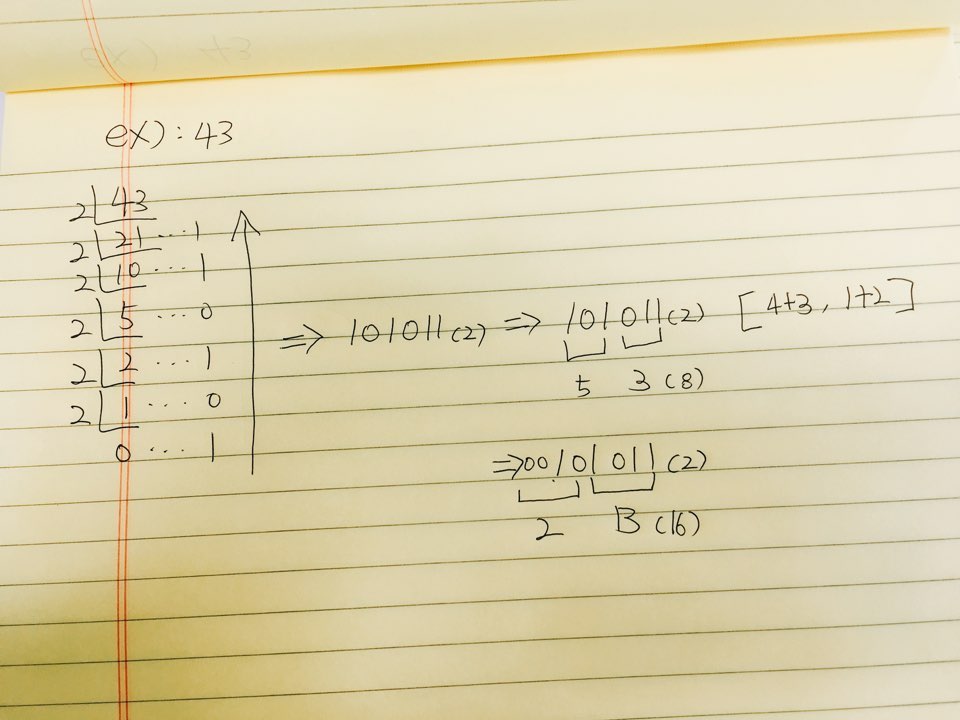
실수를 이진수로 변환
문제는 실수이다.
예를 들어, 십진법에서 1 나누기 3은 0.33333333333333333… 인 무한 소수로 정확하게 떨어지지 않는다.
이와 같이 0.1(십진법)을 이진법으로 변환하게 되면 0.000110011001100110011001100110011001…와 같이 무한 소수로 정확하게 떨어지지 않는다.
컴퓨터의 메모리는 무한하지 않다. 따라서 표현할 수 있는 최대한의 범위 내에서
컴퓨터는 가장 근접한 값, 즉 근사값으로 반올림 처리하여 우리에게 결과를 보여준다. 그리고 이로 인해 위와 같은 오차가 발생하는 것이다.
고정 소수점 방법
정수를 표현하는 비트 수와 소수를 표현하는 비트 수를 미리 정해 놓고, 해당 비트 만큼만 사용해서 숫자를 표현하는 방식
변환 예시는 다음과 같다.
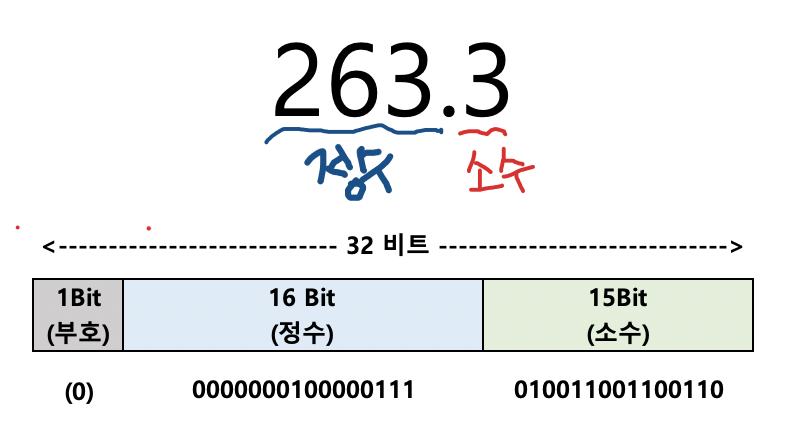
정수인 263을 2진법으로 바꿔서 16bit로 저장하고, 소수인 0.3을 2진법으로 바꿔서 15bit로 저장한다.
즉, 이런 시스템에서는 부호는 +이므로 0이 저장되고, 정수인 263은 16bit를 사용하므로, 0000000100000111이 저장되고, 소수인 0.3은 15bit를 사용하므로, 010011001100110으로 저장이 된다…
고정 소수점 방식은 미리 소수부의 자릿수를 고정시키기 때문에
정수를 표현하는 bit를 늘리면 큰 숫자를 표현할 수 있지만, 정밀한 숫자는 표현이 어렵고,
소수를 표현하는 bit를 늘리면 정밀한 숫자를 표현할 수 있지만, 큰 숫자는 표현이 어렵다.</b>
부동 소수점 방법
소수점의 위치를 고정하지 않고 그 위치를 나타내는 수를 따로 적는 것으로, 유효숫자를 나타내는 가수와 소수점의 위치를 풀이하는 지수로 나누어 표현한다. IEEE 754는 전기 전자 기술자 협회(IEEE)에서 개발한 컴퓨터에서 부동소수점을 표현하는 가장 널리 쓰이는 표준이다.
javascript와 많은 언어들은 이 방식을 사용한다.
실수값을 Floating point 방식으로 2진수로 변환하는 예시!
reference
- 0.1 + 0.2 !== 0.3 잘 설명
https://medium.com/@syalot005006/%EC%9E%90%EB%B0%94%EC%8A%A4%ED%81%AC%EB%A6%BD%ED%8A%B8%EC%9D%98-%EC%8B%A4%EC%88%98-%EA%B3%84%EC%82%B0-%EC%98%A4%EB%A5%98-a72ec3326b50
- 실수 변환 원리를 가장 잘 설명해줌
https://imcts.github.io/javascript-exponent-expression/
- 실수 변환 원리 잘 설명해줌
https://velog.io/@thms200/%EB%B6%80%EB%8F%99%EC%86%8C%EC%88%98%EC%A0%90-0.1-0.1-02-jbk5jrde3a
https://nybounce.wordpress.com/2016/06/30/ieee-754-0-1-0-2-0-30000000000000004-0-1-0-2-%E2%89%A0-0-3/
http://tcpschool.com/cpp/cpp_datatype_floatingPointNumber
https://velog.io/@coin46/0.1-0.2-0.3
http://cjyuko.blogspot.com/2018/05/10-2.html
https://m.blog.naver.com/PostView.nhn?blogId=k97b1114&logNo=140156079889&proxyReferer=https:%2F%2Fwww.google.com%2F
https://medium.com/better-programming/why-is-0-1-0-2-not-equal-to-0-3-in-most-programming-languages-99432310d476