Binary Heaps

Tree의 한 종류

규칙 : 위 층보다 작은 숫자가 위치한다. 만약 밑에 부모보다 큰 수가 자식에 오면 자리가 교체된다.

https://visualgo.net/en/heap

priority queue

높은 수가 부모로 간다는 법칙을 통해 우선순위 큐를 구성할 수 있다. heap의 큰 특징이다 장점이라 할 수 있다.

큰 수가 더 높은 우선순위를 가진다고 하면 heap의 법칙에 따라 나중에 추가되엇어도 높은 곳에 추가되고

위에서부터 차례대로 작업을 수행하면서 내려간다면 이것이 곧 우선순위가 주어진 queue와 같은 움직임이라 할 수 있다.

big O notation

methods	big O notation
lookup	O(N)
insert	O(log N)
(perfect case)	O(1)
delete	O(log N)

Trie

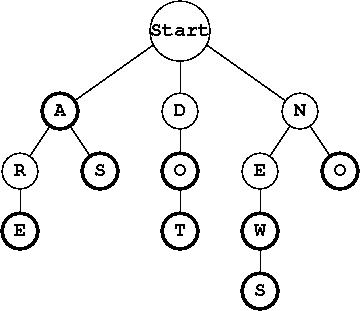
Trie는 보통 text와 함께 쓰이며 searching에 특화된 Tree이다.

search의 종류에 따라 hash table이나 binary search tree 등의 여러 data structure들의 search속도를 능가할 수 있다.

Speed & Space Advantage

Speed : O(length of word)이지만 문자 A를 찾으면 A와 관련된 아래의 Are이나 As를 한번에 찾을 수 있다. 따라서 검색속도가 매우 빠르다.

Space : 단어 하나하나 Are따로 As따로 저장 할 필요없이 A를 저장하고 관련된 문자들을 연결해놓으면 되기 때문에 저장공간이 매우 절약된다.(한마디로 prefix를 사용하면 된다.)

Memory heap And Heap

They have the same name but they really aren’t similar (even conceptually). A memory heap is called a heap in the same way you would refer to a laundry basket as a “heap of clothes”.

This name is used to indicate a somewhat messy place where memory can be allocated and deallocated at will. The data structure (as the Wikipedia link you reference points out) is quite different.

https://stackoverflow.com/questions/1699057/why-are-two-different-concepts-both-called-heap